Braess 의 역설
도로는 "통제를 해야" 길이 덜 막힌다? 얼핏 들으면 말이 안 되는 소리 같아 보인다. 하지만 브라에스의(Braess) 역설에 따르면, 일부 경우에는 추가적인 도로를 건설하거나 기존 도로를 통제할 때, 도로 전체적인 흐름이 더 나빠질 수 있다. 이는 개별 차량이 최적의 경로를 선택하기 위해 자유롭게 움직일 수 있는 상황에서 발생하는 현상으로, 개별 차량이 최단 경로를 택할 때 전체적인 교통 흐름이 최적화되는 것과는 상반된다.
도로 통제에 대한 브라에스 역설은 일부 상황에서 도로를 통제하면 도로 전체적인 흐름이 저하되는 현상을 설명한다. 이 역설은 일반적으로 도로 네트워크에서 발생하는 현상을 설명하는 모델로서 사용된다.

예를 들어, 어떤 도로 네트워크에서 A 지점에서 B 지점으로 가는 경로가 있을 때, 이 경로에는 교차로가 없고 차량의 통행이 원활하게 이루어진다고 가정하자. 하지만 중간에 추가적인 도로가 건설되어 대부분의 차량들이 아래와 같은 다른 경로를 선택할 가능성이 생긴다.

총 걸리는 시간은 20분, 대부분의 운전자들은 최단 시간이 걸리는 도로를 선택하게 될 것이다. 하지만 여기서 문제가 발생하게 된다. 더 많은 사람들이 중간에 새로 생긴 도로를 이용하기 시작하며 점점 교통량은 증가하게 된다.
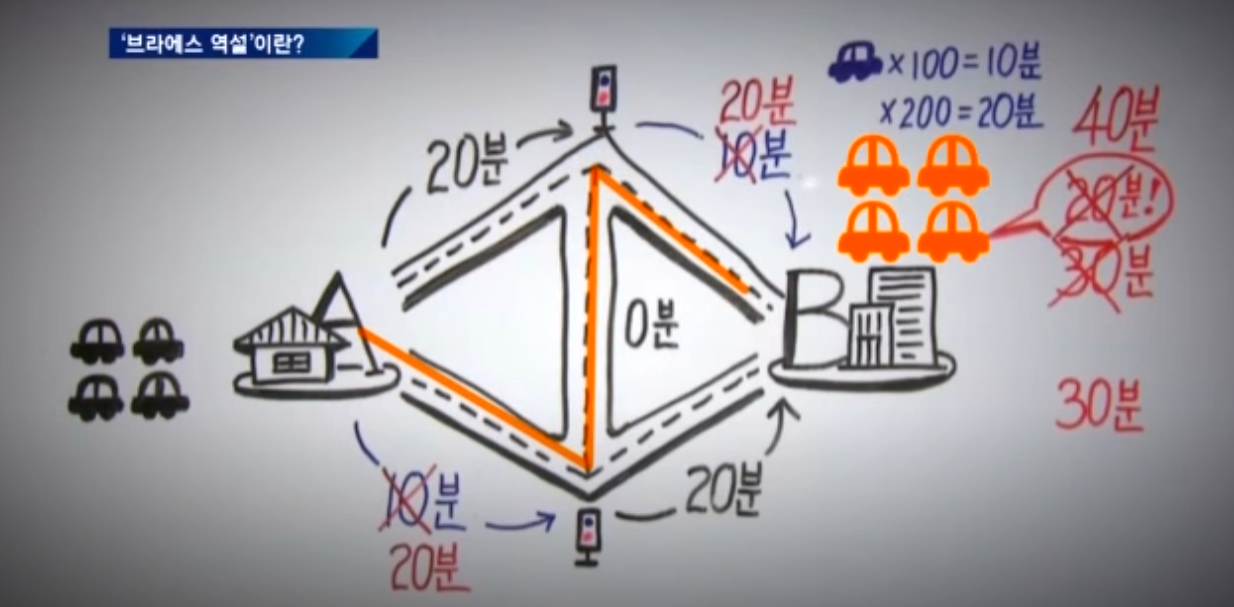
결과로 개별 차량들이 새로운 경로를 통해 이동하게 되면, 새로운 경로에는 교통량이 증가하게 되고, 전체적인 교통 흐름이 악화될 수 있다. 이런 상황에서는 도로를 통제하는 것이 오히려 교통 혼잡을 악화시키는 결과를 초래할 수 있다. 결국에는 위의 그림과 같이 교통량이 증가해서 오히려 20분 + 20분 총 40분이 걸리는 상황이 발생하게 된다.

"도로를 늘리면 오히려 교통혼잡이 는다"는 독일 수학자 브라에스의 역설을 이용해 단순하게 한 가지 경우를 예시로 들었지만 브라에스 역설은 모든 상황에 적용되는 법칙은 아니다. 도로 네트워크의 구성, 교통 흐름의 특성 등 여러 요소에 따라 도로 통제가 도로 전체적인 흐름을 개선할 수도 있다. 따라서 도로 통제 정책을 결정할 때에는 교통처리를 관리하는 엔지니어의 신중한 분석과 평가가 필요하다고 본다.
'Mathematics & Science > 일반수학' 카테고리의 다른 글
| 쉽게 배수 찾는 방법 (3의 배수는 각 자리수의 합이 3의 배수) (1) | 2019.12.26 |
|---|
댓글