검색어 유입에서 생각보다 "풋옵션 만기 시 금액"이라는 검색어 유입이 많아서 쉽게 옵션 결제에 관해 설명하려 한다.
우선 옵션은 선물과 매우 유사하다. 미래의 특정 시점에 (만기 시) 결정될 불확실한 가격에 대해 베팅하는 파생상품이다. 우선 선물거래에 관해서 알고 있다면 이해가 매우 쉬울 것이다. 하지만 선물거래에 관해 알지 못하더라도 이해하기 쉽게 로빈후드 호가창에서 예를 하나 들어보겠다. 우선 풋옵션은 콜옵션에 비해 이해하는데 어려울 수 있으니 콜옵션부터 설명을 하겠다.
콜옵션:
1. 충분한 속도로 주식 가격이 상승하면 콜옵션의 가격도 상승한다.
2. 완만한 속도로 주식 가격이 상승시 콜옵션의 가격은 하락할 수도 있다.
3. 주식 가격 하락시 콜옵션의 가격은 하락한다.
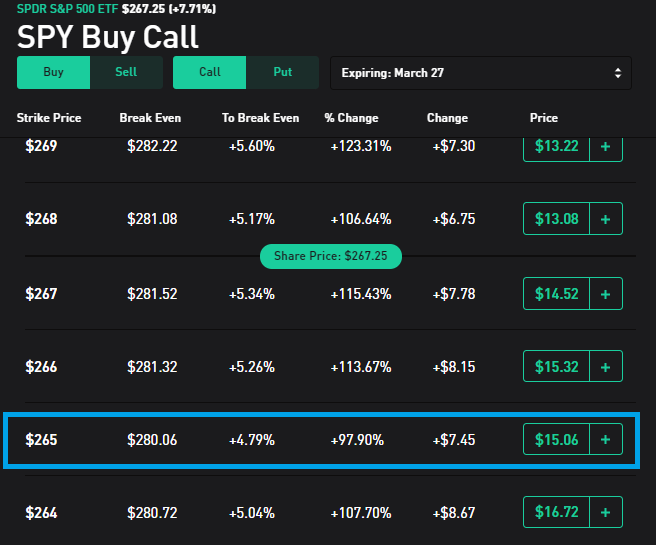
만약에 ETF 가격이 만기일까지 천천히 상승한다면?
자, 여기서 만약에 SPY ETF의 가격이 3월 27일까지 그대로 유지하거나 천천히 상승하면 매수한 콜옵션은 손해일까 이득일까?
정답은 손해이다. 위의 콜옵션 설명에서 2번에 해당하는 경우이다. 완만한 상승 or 보합.
가격 변동이 없을 때 옵션 매수는 시간 잔존가치(Theta)와 변동성 프리미엄(Vega)에서 손해를 보게 된다.
만기일까지 보유할 경우 얼마나 손해를 보는지 단순히 계산해보자.
옵션을 매수를 위해 투자한 금액은 총 $1,506이었다. 우리가 매수한 콜옵션은 결제 가격이 $265.00이기 때문에 종가 $267.25인 경우에 1주당 $265.00에 매수할 수 있는 권리가 생긴다.
즉, $ (267.25 - 265.00)*100 = 결제 시 225불의 차익이 생긴다. 하지만!!! 제일 처음에 우리가 투자한 금액은 총 $1,506이었다.
그러면 결제 차익($225)에서 매입비용($1,506)을 빼면 1,281불의 손실이 발생하게 된다.
$225 - $1,506 = -$1,281
다르게 말하자면, 현재 결제금액 $265에 3월 27일 만기인 콜옵션의 프리미엄은 $1281불이다.
혹은 이 옵션의 가격이 얼마까지 올라가야지 본전이 되는지 알고 싶은가?
그러면 단순히 결제금액과 현재 옵션 가격을 더하면 된다. 로빈후드에서는 Break Even이라 알려준다.
결제가 $265에서 현재 옵션가 $15.06를 더하면 $280.06 이다.
$265+$15.06 =$280.06
(만기일까지 보유 시 이득이 나기 시작하는 가격.)
현재 속마음으로 "와 지금 가격이 265인데 280을 넘지 않으면 무조건 손해?" 사기 아닌가라고 생각하는 사람들 있을 거다.
하지만 기초자산의 가격 변동(Delta)과 변동성 프리미엄(Vega)이 시간 가치 하락(Theta)를 넘어서 상승한다면 만기일 전에 $280에 도달하지 않더라도 충분히 이득을 취할 수 있다.
(자세한 내용은 이글 아래 옵션 가격 변화지표에 대한 링크를 참조하기 바란다.)
풋옵션:
1. 충분한 속도로 주식 가격이 하락하면 풋옵션의 가격은 상승한다.
2. 완만한 속도로 주식 가격이 하락하면 풋옵션의 가격은 하락 할 수도 있다.
3. 주식 가격이 상승시 풋옵션의 가격은 하락한다.

자 여기서는 3월 27일이 만기인 $270 풋옵션을 매수하고 SPY ETF가 아주 조금 떨어져서 $260에 도달했다고 가정해보자. 풋옵션을 매수를 위해 투자한 금액은 총 $1,355이었다. 우리가 매수한 풋옵션은 결제 가격이 $270.00이기 때문에 종가 $260.00인 경우에 1주당 $270.00에 매도할 수 있는 권리가 생긴다.
즉, $ (270.00 - 260.00)*100 = 결제 시 1000불의 차익이 생긴다.
하지만!!! 제일 처음에 우리가 투자한 금액은 총 $1,355이었다.
그러면 결제 차익($1,000)에서 매입비용($1,355)을 빼면 의 손실이 발생하게 된다.
$1,000 - $1,355 = -$355
방향성은 맞추었을지라도 충분한 하락이 발생하지 않아서 만기일까지 보유할 시에 손실이 나는 경우가 발생한다.
다시금 말하지만 간혹 옵션을 홀짝 게임이라 생각하여 바카라에 비교하고는 하는데 옵션은 방향성도 중요하지만 변동성에 투자하는 상품이다.
|
델타 (Delta) |
기초자산 가격 변동에 따른 옵션의 가격 변화율 |
|
세타 (Theta) |
시간이 흐름에 따라 발생하는 옵션 가격의 변화율 |
|
베가 (Vega) |
내재 변동율(IV)에 의해 발생하는 옵션 가격의 변화율 |
위의 내용에서 기초 자산 가격 변동(Delta), 시간 잔존가치(Theta), 변동 성프리미엄(Vega)에 관해서 더 자세히 알고 싶다면 아래 링크를 통해 더 자세한 설명을 확인할 수 있다.
주식의 100배. 레버리지 끝판왕 옵션 Option, 하락 시 엄청난 수익을 안겨다 주는 풋옵션. 델타, 감마, 세타, 베가, 로우.
최근에 인터넷이나 카톡방에서 주식 관련 이야기를 눈팅하다 보면 옵션을 홀짝 바카라 정도로만 생각하시는 분들이 많은 것 같다. 외가 (Out of the Money Option) 옵션을 매수하면 상당한 레버리지를 끌어 올 수..
woogong2.tistory.com
'경제 및 투자 > 옵션 트레이딩' 카테고리의 다른 글
| [2021년 2월7일] 로빈후드, 옵션 양매도 포지션 (Iron Condor) (0) | 2021.02.08 |
|---|---|
| Option Spread 투자 전략 (콜옵션 스프레드). (0) | 2020.10.17 |
| 커버드 콜(Covered Call)을 이용하여 추가 수익 실현해보자. (0) | 2020.07.08 |
| 주식의 100배. 레버리지 끝판왕 옵션 Option, 하락 시 엄청난 수익을 안겨다 주는 풋옵션. 델타, 감마, 세타, 베가, 로우. (0) | 2020.03.12 |
| 주식 하나 없이 상승할 때 이득보는 방법? 풋콜 패러티 (Put-Call Parity) (1) | 2020.03.07 |



댓글