불과 십여 년 전만 해도 남아선호사상이 강해서 한 가정에서 남자아이를 낳을 때까지 계속해서 출산하는 경우가 많았다.
심지어 3대 독자 5대 독자 이런 단어도 있다.
남아선호사상이 강해서 한가정에서 남자아이를 낳을 때까지 계속해서 아이를 낳게 된다면 전체 인구로 보았을 때 여자의 인구수가 남자 인구수보다 더 많아지게 될까?
|
1번째 시도 |
2번째 |
3번째 |
4번째 |
확률 |
|
아들 |
1/2 |
|||
|
딸 |
아들 |
1/4 |
||
|
딸 |
딸 |
아들 |
1/8 |
|
|
딸 |
딸 |
딸 |
아들 |
1/16 |
우선 표를 확인해보자.. 이해해도 뭐 그래서 어쩌라는 건지? 라는 생각이 들 것이다.
|
이해하기 쉽게 마을에 총 8가구가 있다고 가정해보자. (결과가 확률에 비슷하게 나온다는 가정으로 계산) |
| 1번째 시도에서 4가구는 아들, 4가구는 딸을 낳을 것이다. (4가구는 출산 Stop) |
| 2번째 시도에서는 딸을 낳은 4가구가 다시 시도해서 2가구가 아들, 2가구가 딸 (2가구 출산 Stop) |
| 3번째 시도에서는 2번째에서 아들을 낳지 못한 2가구가 다시 시도, 1가구 아들 1가구 딸 |
| 4번째 시도에서는 아들을 갖지 못한 1가구가 다시 시도 1/2 확률 |
| 위의 결과를 남자 여자 수로 생각해보면 |
| 1번째 시도에서는 남자4+여자4 |
| 2번째 시도에서는 남자2+여자2 |
| 3번째 시도에서는 남자1+여자1 |
| 4번째 시도에서는 남자0.5+여자0.5 (0.5명이라는 게 말이 안 되지만 확률상) |
매 시도마다 남자와 여자 수가 같음을 알 수 있다.
남자가 나올 확률을 계산해보면 아래 표와 같다.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 남자확률 |
| 아들 | 1/2 | ||||||||
| 딸 | 아들 | 1/4 | |||||||
| 딸 | 딸 | 아들 | 1/8 | ||||||
| 딸 | 딸 | 딸 | 아들 | 1/16 | |||||
| 딸 | 딸 | 딸 | 딸 | 아들 | 1/32 | ||||
| 딸 | 딸 | 딸 | 딸 | 딸 | 아들 | 1/64 | |||
| 딸 | 딸 | 딸 | 딸 | 딸 | 딸 | 아들 | 1/128 | ||
| 딸 | 딸 | 딸 | 딸 | 딸 | 딸 | 딸 | 아들 | 1/256 | |
| 딸 | 딸 | 딸 | 딸 | 딸 | 딸 | 딸 | 딸 | 아들 | 1/512 |
계속해서 2의 배수로 확률이 감소하는 것을 알 수 있다. 표를 수식으로 정리하자면
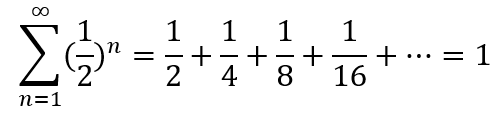
한 가구에서 남자와 여자를 가질 기댓값(평균값)은 1이다.
큰 관점에서 보게 된다면 남아선호사상으로 남자아이가 나올 때까지 아이를 낳게 되면 한 가정은 딸 1명 그리고 아들 1명을 가지게 된다.
'Mathematics & Science > 확률' 카테고리의 다른 글
| Multiverse 멀티버스 과연 존재하는 걸까? (Feat. 다중 우주론) (0) | 2023.02.12 |
|---|---|
| 룰렛에서 20번 빨간색 나오는 경우 다음은 검정색? (feat. 도박사의 오류) (1) | 2020.08.05 |
| 몬티 홀 문제, 선택을 바꾸면 당첨 확률이 올라간다! (0) | 2020.02.14 |
| [확률] 이항분포, Binomial distribution (0) | 2019.10.11 |




댓글